
Coastal pressures
- 2.27 > As seen in this view of Cancún, Mexico, the effects of mass tourism have obliterated the pristine appearance of many coastal regions. This kind of overuse can blight the recreational value of these areas.
Overuse harms habitats
The appeal of the coasts is explained to a great extent by the large number of ecosystem services that they provide. In past decades the power of this attraction led to many coastal regions becoming increasingly heavily populated and pressured beyond their carrying capacity – be it through excessive fishery or the challenges of wastewater treatment. By using the coasts unsustainably, people harm themselves in the end because there will come a time when certain ecosystem services can no longer be provided.
One example is the development of mass tourism in many locations. Coastal regions want to attract holidaymakers to their beaches with attractive landscapes and clean water, yet obtrusive hotel-building destroys the pristine appearance of the landscape, while immense quantities of wastewater from the hotel complexes cause water pollution. This is how overuse blights the recreational value of a landscape, undermining its provision of cultural ecosystem services.Hard-to-pinpoint threats
Some forms of overuse are not always easy to identify and measure. Humans and the environment are closely interwoven in socio-ecological systems. Coastal regions extend over vast areas between land and sea and are very difficult to define in precise spatial terms. There can also be a lengthy time lag between cause and effect.
One example is the industrial use of polychlorinated biphenyls (PCBs): chlorine compounds that were used until the end of the last century in transformers, in hy-draulic fluids and as softeners in sealants and plastics. Because they were applied in such diverse uses, significant quantities found their way into the environment. Only in the early 1970s was it recognized that the substances are toxic and have carcinogenic effects. Moreover, it was observed that in sea mammals such as seals they cause pathological changes to the uterus. This has resulted in a drastic decline in the number of successful seal births in the North Sea and the Baltic, particularly since the 1970s. Finally, in 2001 the use of PCBs was prohibited by the Stockholm Convention, an international treaty to protect the environment from particularly dangerous chemicals. Thus, several decades elapsed between the actual cause, the emergence of the environmental problem, the identification of the substances and the systematic ban on their use.
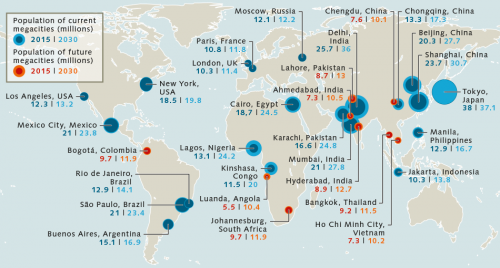
Ever expanding megacities
Within socio-ecological systems where people live in large numbers or sources of pressure are multifarious, the interactions can be especially complex and in many cases difficult to discern. Today this applies particularly to coastal megacities of over 10 million inhabitants. Such regions are characterized by high population density and high-density building development. Many people need to be supplied with fresh water, food and electricity, which imposes high demands upon infrastructure, logistics and waste disposal. Because people from poorer rural regions inland are constantly moving to the coastal megacities in search of work or training, these metropolitan centres will continue to grow in future – above all in Africa, South America and South East Asia.
- 2.28 > Many of the megacities of the future, cities of over 10 million inhabitants, are in Asia and Africa.
Aquifer The term “aquifer” denotes a subsurface body of rock containing pore spaces through which groundwater flows.
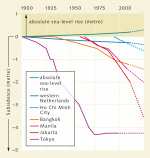 2.30 > Tokyo managed to halt its land subsidence from the mid-1970s, unlike most other cities.
2.30 > Tokyo managed to halt its land subsidence from the mid-1970s, unlike most other cities.- One of the biggest problems in the wake of this continuous urbanization has been the increasing frequency of floods affecting entire urban districts. Flooding can be caused both by heavy rainfall events and by storm surges in the sea level. Apart from the immense economic damage caused by floods, they pose a very real risk to life and limb. Interestingly, so far these have been attributable not so much to global climate change and sea-level rise than to bad urban planning. The following causes have been identified:
- Subsidence due to building density: the construction of high-rise buildings and other large structures has significantly increased the load on the ground. Under the heavy weight, the densely built-up sites slowly subside.
- Subsidence due to groundwater abstraction: because ponds, lakes and rivers at ground level in many coastal cities are heavily polluted by untreated wastewater and detritus, they cannot be used as sources of drinking water. Drinking water for many millions of inhabitants therefore has to be abstracted from the groundwater in the deeper geological rock layer, the aquifer. Since groundwater normally acts as a natural abutment against the downward force of buildings, pumping it away in large quantities exacerbates the subsidence of densely built-up areas. Construction measures themselves also lead to a fall in the groundwater level. Deep excavations are made for large buildings and any water that penetrates is pumped out, with the result that the ground in the excavations settles and the pore volume that was previously filled by the groundwater shrinks. The land surface then sinks.
- Construction on low-lying river catchments and marshlands: many of the migrants to cities from poorer rural regions settle at the growing periphery of the cities in what are known as informal settlements. These are often located in low-lying areas that are unsuitable for building development, which are frequently along the banks of rivers or on marshes and meadows at especially high risk of flooding.
- Poor sewer construction: in many cities, developments have been built across natural watercourses or flood-prone areas such as alluvial plains. As a result, natural rainwater drainage areas have disappeared in many places. Added to that, surfaces have been sealed by the construction development so that rainwater no longer has much seepage area, but drains away torrentially instead.
- Natural subsidence: in some coastal regions the land is slowly sinking naturally. There can be a number of causes for this. For example, in some areas the land mass may slowly subside due to the movement of a continental plate. In other coastal areas, particularly in river deltas, the ground sinks because sediment layers become more densely packed over time and sag under their own weight.
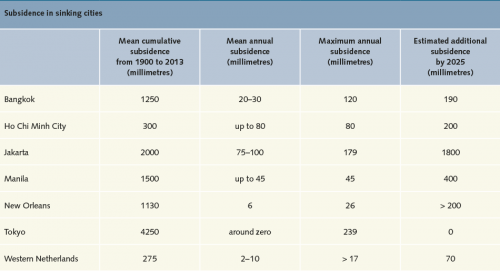
- 2.29 > Many of the world’s largest cities are sinking today, primarily due to groundwater abstraction and massive building development. In many cities this subsidence will continue into the future.
-
2.31 > Inundation of an entire industrial zone in the province of Ayutthaya, north of the Thai capital of Bangkok, in November 2011. Among those affected by the disaster is a Japanese car manufacturer based there.
A sinking metropolis
An extreme example of a sinking city is Jakarta, the capital of Indonesia, which is currently the fastest sinking metropolis in the world. Particularly since the 1980s the city has grown drastically in terms of both population and road and building construction – especially high-rise buildings. In 2015 Jakarta already had at least 10 million inhabitants, and its population is forecast to reach 13.8 million by the year 2030.
Jakarta is in a very low-lying region, partly on peaty soils. The densely developed northern area, with its many high-rise buildings, and the commercial centre in particular are sinking in the soft subsurface – currently by up to 10 centimetres a year. The abstraction of groundwater for drinking water supply is also contributing to this effect, and it is feared that the sinking will accelerate. Without countermeasures and a reduction of groundwater abstraction, by the year 2025 parts of Jakarta are likely to have sunk by a further 180 centimetres.
Floods occur with growing frequency, leaving the city’s highways and commercial centre half a metre under water, both after heavy rainfall events and higher than usual sea water levels. Natural watershed and floodplain areas have been built upon repeatedly over time so that rainwater has almost nowhere to seep away. The alarming fact today is that more and more people are affected by the floods. New arrivals in the city predominantly settle close to the economically attractive north of the city. This increases their prospects of finding work or reduces the length of the commute to their workplaces.
- 2.32 > Jakarta is currently the world’s fastest sinking metropolis. Because the city pumps groundwater on a large scale for its drinking water supply, the modern city centre is subsiding dramatically.

- Flooding also has grave financial consequences, as seen for example in the year 2007, when a good one-third of Jakarta’s area was inundated after severe rainfalls. Around 300,000 people lost their homes. The damage to infrastructure and buildings amounted to the equivalent of some 860 million US dollars.
Floods affect not just the city itself but also, indirectly, its surroundings – the city of Jakarta is part of an urban conurbation, also comprising the adjacent cities of Bogor, Depok, Tangerang and Bekasi. This is one of the largest agglomerations in the world, reflected in the name it is commonly known by today: the acronym “Jabodetabek”. Every year around 250,000 people move into this agglomeration, which means that about 35 million people will be living there in the year 2020.
Every time that Jakarta is flooded, it causes transport chaos in the neighbouring areas. And another issue affects the region as a whole: if diseases or epidemics break out in the flooded areas because of the standing dirty water, these can rapidly spread throughout the whole of Jabodetabek.
A giant bird to defend Jakarta
In order to defend the city of Jakarta from greater floods in future, the Indonesian authorities are currently planning to create hydraulically filled islands that will shut off the approximately 35-kilometre wide Bay of Jakarta and be developed with residential, office and hotel complexes. The largest island alone is 10 kilometres long and will be given the form of a garuda bird with wings spread wide, the emblem of Indonesia. But resistance is stirring within the population. Wastewater could collect in the artificial lagoon landscape because there will barely be anywhere for it to flow into the open sea. Diseases could spread. The small-scale fishers fear losing their livelihoods because in future they will have to travel many kilometres further offshore in order to reach fishing grounds. But that is not possible, argue the fishers, since they only possess simple boats which are often in poor condition and not suitable for longer trips out to sea.
- 2.33 > As a defence against flooding, there are plans to create artificial islands off the coast of Jakarta by hydraulic filling. The largest island will be 10 kilometres long and shaped like Indonesia’s emblematic bird. But the project is controversial. It is feared that wastewater could accumulate in the artificial lagoon, ruining the livelihoods of fishers.

- Construction projects on land which are planned in the course of the hydraulic filling are another major source of potential conflict. The intention is to construct new office, business and residential quarters along the shoreline. In the interim, residents who previously lived in simple shacks and houses in this area are being resettled. Although they are obtaining cheap living space in high-rise buildings in other districts of Jakarta, how can they possibly be compensated for the impending loss of their culture and identity? If the fishers are resettled inland, closer to industrial plants and factories, they can hardly continue in their traditional occupation: fishers will turn into factory workers.
Doubly threatened – by rains and storm surges
Another example of a sinking coastal metropolis that is also plagued by flooding is Manila, the capital of the Philippines. It is likewise threatened by heavy rainfall events and storm-induced high seawater levels. Between 1900 and 2013, parts of Manila sank by 1.5 metres, and further subsidence of around 40 centimetres is expected by the year 2025. This is worrying because Manila is in a region that is often affected by typhoons, huge cyclonic storms. They bring large quantities of rain and churn up the sea so violently that huge breaking waves arise. Typhoon Ketsana in 2009 was a cyclone of catastrophic proportions. The rain and the storm surge inundated some districts of Manila with 2 metres of floodwater.
The fact that flooding is increasingly affecting coastal cities that are not notably subsiding is demonstrated by the example of Mumbai. A large-scale flood hit the Indian megacity on 26 July 2005, when almost 950 millimetres of rain fell within a 24-hour period. That is roughly equivalent to the total volume that normally falls in Mumbai during the entire month of July. In the hour from 15.30 to 16.30 alone, there was 190 millimetres of rain. Since this coincided with a relatively high sea tide, the rainwater could barely seep away and instead backed up in the drains and particularly in the River Mithi which flows through the middle of the city.
Whereas most previous flooding had only affected the unauthorized (informal) settlements on the city periphery, this time the city centre was also hit, and the water rose by more than 1 metre in next to no time. Streets, shops and office buildings were inundated and traffic came to a complete standstill for many hours. In the end 22 per cent of Mumbai’s area was flooded. The flood that day took a tragic toll: over 400 dead and around 100,000 badly damaged homes and businesses. 30,000 vehicles were reduced to scrap metal.
The analysis of the events made it clear that such large-scale flooding in Mumbai could only have happened because major swathes of the natural inundation areas along the rivers had gradually been sealed over, partly by the construction of informal settlements and partly in the course of official projects like the extension of the airport. Moreover, many watercourses were blocked with waste and building debris, impeding the rainwater’s run-off. Elsewhere, rainwater sewers were poorly maintained, river banks had slipped and concrete walls collapsed.
USA also has self-inflicted problems
From a worldwide comparison of coastal metropolises, it is clear that the cities worst affected by flooding are mainly megacities in emerging economies. Experts attribute this to the fact that the required standards are not always adhered to in the planning of structures – particularly with regard to forward-looking land-use planning, disaster preparedness, and functional infrastructure, which includes such features as flood channels, a functioning sewerage system, flood banks and flood control barriers. On the other hand, cities in industrialized countries certainly also have to contend with subsidence. That is evident from the New Orleans conurbation, for example, in which around 1 million people live. New Orleans is in the US state of Louisiana, directly in the Mississippi Delta. Between 1900 and 2013 the city sank by a full 1 metre and is subsiding every year by a further 6 to 26 millimetres.
This is happening for several reasons. As in other affected coastal cities, the abstraction of groundwater plays a part in the subsidence – but how much of a part is very difficult to assess, because the particular characteristics of the soil in New Orleans give rise to another phenomenon: if the groundwater table falls, oxygen from the air penetrates deeper ground layers and activates the soil bacteria that live there. These decompose soil organic matter. Since the soil contains large quantities of organic material that has been carried into the delta by the Mississippi over centuries, the bacteria find large amounts to decompose. This loss of organic substance contributes substantially to the subsidence.
Additionally, in the region around New Orleans, the drilling of petroleum and natural gas and the emptying of those deposits are also causing the ground to sink. The loss of sediment that used to be transported into the delta by the Mississippi should not be underestimated, either. Today, because it is slowed down by numerous weirs, the Mississippi carries distinctly less sediment into the sea. The old sediment packages deposited in the delta are so heavy that the delta is slowly subsiding naturally. Whereas this subsidence used to be evened out by fresh sediment from the Mississippi, today the markedly reduced sediment load is far from sufficient to compensate.
- 2.34 > Hurricane Katrina struck the southeast of the USA in late August 2005. Months later, traces of the destruction were still plain to see.

- These problems had been known about for decades, just like the fact that New Orleans was vulnerable to flooding in the event of even moderately severe storms. Experts had last published a warning in a scientific journal in 2003 about the consequences of severe hurricanes, which often threaten the coast on the Gulf of Mexico in the summer months. The existing flood control works were too low, and others were badly designed, maintained or constructed, their report read. The authorities had in fact planned a hurricane protection system, but due to a shortage of funding it was not built. In the view of experts, even this protection system would have failed because it would have been constructed according to outdated and unduly low design criteria.
Thus, New Orleans was relatively poorly protected when the extremely forceful Hurricane Katrina hit the city at the end of August 2005. It caused a 7-metre rise in the coastal water level. Consequently the flood banks (levees) were breached in around 50 places and the city, which lies in a hollow, filled up with water. Only after that did the authorities react and decide to construct a modern and effective flood protection system, the Hurricane and Storm Damage Risk Reduction System (HSDRRS). This was completed in 2011. It includes higher and more resilient levees and flood control barriers as well as floodgates and emergency pumps at the outlets of the pipes that drain runoff from New Orleans. These measures have considerably reduced the risk of major flooding.
Furthermore in 2012 the US authorities passed a new master plan for the protection of the delta, which will help to protect not only the city of New Orleans but the entire delta region from hurricanes and especially floods in future. A complete package of measures, including dredging works or the pumping of sediment, will allow the delta to grow again over the next 50 years. A good 700 square kilometres of new delta will be created in this way. Added to that will be 500 square kilometres of salt marshes to temper the force of the waves in the event of storms and hurricanes.
Halting the subsidence
The examples of Tokyo and Shanghai demonstrate that the subsidence of a city can be stopped if appropriate action is taken. After parts of the Japanese capital had subsided by around 4 metres since 1900, the decision was taken in the late 1960s to drastically restrict groundwater abstraction. Thereupon the soil strata carrying the groundwater slowly filled up again, so that towards the mid-1970s the subsidence had already been halted.
The Chinese metropolis of Shanghai was faced with similar problems. Its response was not only to heavily regulate groundwater abstraction but also to deploy pump- ing technology, which permitted more rapid replenishment of the groundwater reservoirs with water.
- 2.35 > In the past 40 years the Pearl River Delta in China has developed from an agricultural to a highly industrialized and heavily populated region. The left side of the photomontage is a satellite image from the year 1979, and the right side of the image dates from 2003. Vegetation is shown in red and built-up areas in grey. Watercourses can be seen in blue.
The largest agglomeration on Earth
The development and settlement of coastal areas is probably the most conspicuous change to these habitats. In many cases species-rich wetland biotopes like mudflats and salt meadows, marshes and peatlands have been dried out and irreparably destroyed by construction measures. An extreme example of this urbanization in coastal wetlands is the Pearl River Delta in the middle of the coastal province of Guangdong in the south of China. This is the location of a huge agglomeration consisting of eleven cities, including Hong Kong and Macao. The entire region, covering an area of almost 40,000 square kilometres, is almost the size of the Netherlands.
The region comprises several Special Economic Zones and has undergone a rapid economic upturn since the 1970s. Back then the delta was still characterized by small villages and expansive wetlands, but by the year 2000 the increasingly urban area that formed within it through the merging of the cities took up 3500 square kilometres, which is roughly four times the area of Berlin. Today the drained area covers as much as 4500 square kilometres and the population density is immense. Currently around 60 million people live in the Pearl River Delta – around 3.5 times more than in the Netherlands, which is a densely settled country by European standards. Thus, within a few decades it has developed into the most highly populated agglomeration on Earth. Experts expect growth in this region to persist until the Pearl River Delta is home to around 100 million people by 2030.
With the drainage and redevelopment of the wetland areas, the habitats of many amphibians and birds have disappeared. Furthermore, as a consequence of water pollution, today around 90 fish species in this area are threatened. Aside from that, many river branches in the region carry less water, particularly during the dry months, since numerous dams and power plants were built for drinking water abstraction and electricity generation. Overall this means that considerably less freshwater flows into the delta, and at times when sea levels are high, such as spring tides or storm surges, seawater can penetrate deeper into the delta. Plants and animals that are not adapted to brackish water or higher salt content retreat from the affected zones. The habitat is changing enormously.
 2.36 > The Chinese sturgeon Acipenser sinensis is considered to be at acute risk of extinction.
2.36 > The Chinese sturgeon Acipenser sinensis is considered to be at acute risk of extinction.- Another consequence of dam construction is to interrupt the upstream migration routes of some fish species between the sea and their spawning grounds. In the opinion of experts, this substantially contributed to the collapse of stocks of the threatened Chinese sturgeon Acipenser sinensis, for example.
The removal of sand and stones for building projects represents another extreme case of interference with nature. The building material is taken from the river beds with dredgers and special ships. This alters the rivers’ flow regimes, which in turn leads to changes in the composition of species assemblages. Many water organisms lose their breeding and spawning sites as a result of dredging works.
Big business built on sand
It is not just in China that sand and minerals are extracted but in many of the world’s regions. According to estimates by the United Nations Environment Programme (UNEP), every year between 47 and 59 billion tonnes of minerals are mined worldwide, of which sand, gravel and crushed rock make up between 68 and 85 per cent. Since there is no standardized recording of the statistics, the quantities can only be estimated approximately. Between 25 and 30 billion tonnes of sand are needed for the cement industry alone. But in numerous places this colossal demand entails major encroachments on the landscape. Such resource extraction is therefore viewed very critically in many regions. In South Africa, for instance, dune sand is extracted for the construction industry. Critics fear that the coasts will be less well protected as a result because dunes are a natural bulwark against the breaking waves. In India fishers are protesting against sand extraction from beaches. They are critical that the dredging up of suspended sediments is driving fish away. For the local small fishers, this means the loss of their livelihood.
Seagrass meadows
Characteristic plant communities which typically grow in sandy sediment in coastal waters and on tidal flats. They have long, herb-like fronds and thus resemble – but are unrelated to – the grasses that grow onshore. They are important habitats, providing young fish with food and protection from predators. Various species of fish lay their eggs directly on seagrass, so these meadows are often key nurseries for fish. They are also a vital foraging ground for birds, such as Brent geese during their autumn migration across Western Europe’s Wadden Sea.Extra Info Reef fishing at the limit – Spermonde Archipelago

- Similarly in Indonesia and Cambodia, the removal of large quantities of sand – mainly for export to Singa-
pore – has led to major destruction of the coasts, which prompted the government of Indonesia to prohibit the export of sand completely in 2008 while the government of Cambodia markedly restricted official exports in 2009. Nevertheless, sand extraction in Cambodia is continuing on a grand scale. Cambodian nature conservation organizations draw attention to the fact that sand is being traded in some cases by Mafioso groups. They complain that Cambodian authorities are not carrying out any controls. To what extent the government has secretly awarded permits for this extraction, or how far the corruption of officials is involved, remain unanswered questions. Sand is being extracted using suction dredgers in a coastal protection area in the Koh Kong region west of the capital Phnom Penh, among other sites. This is destroying mangroves and seagrass meadows – important habitats for the dugong, a species of sea cow.
Turning now to Singapore, the South East Asian city-state is an extreme example of sand imports. Being an island, Singapore constantly requires sand for the enlargement of its urban area. Between 1995 and 2014, around 500 million tonnes of sand were imported – for the most part from Indonesia and Cambodia. Since those countries adopted their export restrictions, sand has been imported to Singapore illegally, say the Cambodian nature conservation organizations.Overexploited fishing grounds
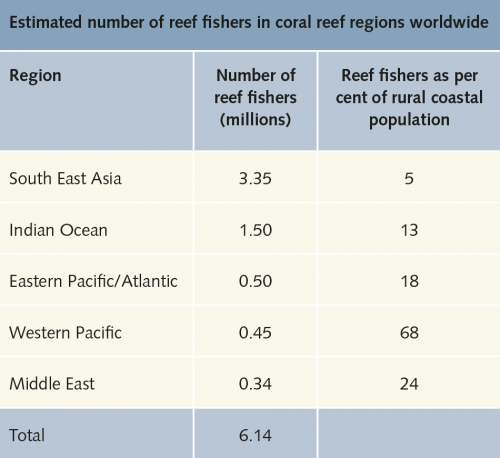
The overexploitation of coastal areas is particularly evident when it comes to fishing. Not only is too much fish taken from the oceans, but fishing can also destroy marine habitats such as coral reefs. Humans take more fish out of the sea than the sea can continue to produce. As a result, fish stocks decline over time. It is not possible to state exactly the degree to which coastal regions are overfished, since the Food and Agriculture Organization of the United Nations (FAO) does not differentiate in detail between coastal fisheries and deep sea fishing. However, given that coastal waters worldwide constitute the most productive marine regions they no doubt provide the bulk of fish, and fisheries experts believe that they are the most intensively fished waters. According to current FAO data roughly 30 per cent of all commercially fished stocks worldwide are overfished. Given that there are more than 38 million fishers in the world who could lose their livelihoods or their food source, this situation is alarming. At particular risk are the small-scale fisheries on which approximately 20 million fishers depend in the developing countries alone, where fishing makes a significant contribution to the food supply and livelihoods of coastal people. In the tropics, small-scale fishing is primarily carried out on coral reefs. The number of coral reef fishers is estimated to be in the order of 6 million, 1.7 million of whom live in Indonesia, roughly 950,000 in India and 910,000 in the Philippines. Roughly half of the 6 million reef fishers primarily dive for sea cucumbers. These sausage-shaped echinoderms are related to starfish and are exported to Hong Kong in particular where the dried animals are valued and traded as medicine.
In many areas, coral reef fisheries are not currently managed in a sustainable manner. Not only are their stocks being overfished but the reefs are also damaged in a variety of ways. This is tragic as in the long-term people are destroying their own livelihoods.
- 2.38 > South East Asia, and especially Indonesia, has particularly high numbers of reef fishers. However, as a ratio of reef fishers to rural coastal population, Western Pacific island nations have the highest percentage, as these islands offer scarcely any other livelihood options.
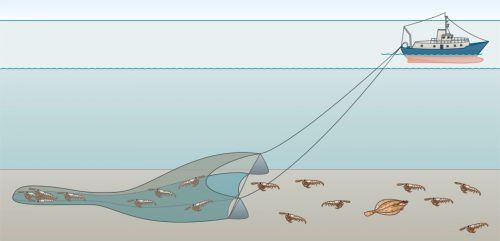
Stronger engines, greater destruction
Just how strongly intensive fishing impacts on inshore marine areas can be illustrated by the example of the Belgian, German and Dutch North Sea coast where fishing has very strongly altered seafloor habitats over the last hundred years. In these habitats, flatfish species such as dab, plaice and sole that camouflage themselves by partially burying themselves in the soft seabed are caught with bag-like bottom trawls that are dragged across the sea floor on heavy metal frames. These beam trawls and the chains attached to them are designed to penetrate and basically plough up the top few centimetres of the soft seabed as they are towed along.
In the nineteenth and early twentieth century, flatfish were in many areas still caught using small rowing or sailing boats and correspondingly small beam trawls. However, with the introduction of larger, motorized vessels ever larger beam trawls came to be used in the North Sea. Due to their high weight and the attached chains they plough up the seafloor and crush many of the larger benthic organisms. Studies conducted in Belgium, Germany and the Netherlands have shown that this is the reason for the significant decline in larger, long-lived or sensitive benthic species observed since the middle of the last century. The sensitive organisms include the tiny moss animals, organisms that form delicate colonies on the seafloor, some of which resemble corals in shape.
- 2.42 > The English port town of North Shields in 1904. At the beginning of the twentieth century North Sea fishing was still mostly carried out by means of sailing boats.

- Ocean quahog populations are also affected. This species of clam lives buried only a few centimetres deep in the ocean floor and their shells therefore are easily crushed by beam trawls. Normally, ocean quahog can grow to a size of more than 10 centimetres and live for up to 120 years. But as a result of intensive beam trawling they have been decimated in the inshore areas of the North Sea; with multiple beam trawl passes per year and area the populations are hardly given a chance to recover. Today the heavily fished areas are dominated by fast-growing bristle worms and small bivalves such as the tellinids which measure only 1 to 2 centimetres in size. Starfish and hermit crabs have also increased in abundance, both of which feed on the remains of the organisms killed by beam trawls. Hermit crabs are protected from beam trawls as they reside in thick-walled empty seashells. Starfish survive as they are relatively robust; if any of their arms are severed by a beam trawl they can regenerate these arms and survive.
The end of a clam paradise
Just how fishing can destroy an almost paradisic habitat, marine biologists were able to document using unique historic datasets for the Dogger Bank, a relatively shallow area in the North Sea. The Dogger Bank has only been used for fishing since the middle of the last century, primarily to catch sandeels to be processed into fishmeal. Thanks to a detailed study conducted by British researchers in the 1920s we have knowledge of the then pristine condition of this region. At the time, the scientists found extensive mussel banks on the Dogger Bank’s seafloor that hosted a multitude of large bivalve species – the thick shelled trough shell Spisula subtruncata for example or its up to 6 centimetres long relative Mactra stultorum. Another frequent species was the common necklace shell, a predatory species feeding on the two trough shell species. Large numbers of moss animals and colourful sea anemones settled on the mussel banks, while many different crustaceans and fish species used this habitat as their hunting ground. As a result of the intensive sandeel fisheries the mussel banks have disappeared and have been replaced by monotonous sandy areas. Comparative studies conducted in recent years have shown that the two trough shell species now only occur as juveniles, if at all. They develop from larvae carried to the Dogger Bank by currents passing from other regions of the North Sea. Adult specimens have become very rare. Today the biocoenoses are dominated by small hardy species instead, such as small amphipods, small tellinids or brittle stars, a particular type of starfish with long thin arms.
- 2.43 > Beam trawls are bottom trawling nets that are dragged along the seafloor on heavy metal frames. They kill many of the animals living on and in the seafloor.
The biocoenosis as a functional unit
In how far such changes should be considered acceptable or intolerable is a matter of perspective. While the loss of original biocoenoses is indeed regrettable, ecologists say that first and foremost it is primarily important for a habitat to continue to function as a whole. The term used by experts in this respect is biodiversity and ecosystem functioning (BEF), i.e. the functioning of a habitat including its potentially changing suit of species. One example of such a function is the cleaning function performed by bivalves as they draw seawater into their shells and filter it. Both small and large bivalves can perform this cleaning function. For the Dogger Bank this means that at present many small tellinids perform the cleaning function previously performed by the significantly larger trough shells of old. The cleaning function is not lost despite the fact that the habitat has changed significantly.
However, as recent studies conducted at the Dogger Bank have shown, the biocoenoses in the area are no longer impacted just by fishing alone but also by climate change. Species at home at more southerly latitudes are slowly migrating into cooler, more northern marine areas such as the North Sea. It remains uncertain how such migrations will impact on the area’s diversity and ecosystem functioning.
- 2.44 > Mussel graveyard in the Finnish Baltic Sea: Once the water’s oxygen concentration had fallen below a critical threshold, the sand gapers emerged from the seafloor sediment in an attempt to reach fresh water. Due to the low oxygen concentrations they perished nonetheless.

Nutrients destabilize the ecosystem
Habitats lose their function when changes exceed stress limits. In many areas, one of today’s major stressors is eutrophication, i.e. the enrichment of a water body with nutrients. These nutrients originate in wastewater contaminated with faecal matter or in the form of crop fertilizers applied to fields from where they reach rivers and are transported into the sea. Where there is an oversupply of nutrients, algal growth can be so rapid that it results in algal blooms. The more abundant the algae, the greater is the quantity of algae that die at some point, and the more intensive is their subsequent decomposition by oxygen-consuming microorganisms and therefore overall oxygen consumption. As a result, oxygen-deficient or oxygen-depleted zones can develop in coastal waters in which fish, crustaceans and molluscs can no longer survive.
For a number of decades now such zones have been observed in many places worldwide, for example on the west coast of India, in Chesapeake Bay on the eastern US seaboard and in the Gulf of Bohai on the east coast of China. The oxygen-depleted zones often develop at greater water depths where wind and waves cannot mix the water and enrich it with atmospheric oxygen. In recent years, these zones have been found on the German Baltic coast during the summer and also in inshore areas at depths of just a few metres. The lack of oxygen in shallow coastal areas is particularly problematic as it also kills benthic organisms the activities of which would normally contribute to the decomposition of nutrients in marine waters and would thus combat eutrophication. These organisms include bivalves and worms that live burrowed into the seafloor substrate into which they fan fresh water. The many passages increase the overall area available for benthic microorganisms to break down nitrogen compounds. But if these bivalves and worms die, this filter function is lost, resulting in a negative feedback loop in oxygen-deficient coastal areas: Oxygen-deficiency results in the soil organisms’ death, which adversely impacts the substrates’ cleaning function and in turn leads to a further deterioration in water quality.
Nutrient loads from aquaculture
While coastal waters in most countries are primarily impacted by nutrients from agricultural sources, intensive aquaculture exacerbates the problem of eutrophication in many regions. This is particularly true for China’s coastal areas where aquaculture installations are lined up like pearls on a string, such as is the case on Hainan Island, a Special Economic Zone in China’s tropical south and a destination for many domestic tourists.
With an area of 34,000 square kilometres, Hainan is larger than Sicily. It is the largest island of the People’s Republic. A wide mangrove belt constitutes the natural coastal vegetation, followed on the seaward side by shallow sandy areas covered by seagrass meadows and, further seaward still, by extensive coral reefs. In recent years, this natural zonation of mangroves, seagrass and corals has, in part, been hugely altered as a result of the expansion of aquaculture. An entire biodiverse ecosystem was lost when the mangroves were cut down. Moreover, nutrients from aquaculture installations, primarily in the form of faeces and excess feed, can now flow directly into the sea. Where normally the mangroves would have taken up much of this nutrient load through their root system, the nutrients now directly enter the seagrass meadows. It is a known fact that under the influence of high nutrient loads small algae thrive that overgrow and ultimately kill the seagrass. Moreover, the oxygen-deficiency caused by eutrophication results in a drop in oxygen concentrations not only in the water column but also in the seafloor, creating conditions that lead to the production of toxic compounds in the sediment which can be lethal to seagrass. Studies are currently being undertaken to determine the extent to which the seagrass meadows in the Hainan area have already died off or may die off in the future.
Just how much of the nutrient load the seagrass meadows can absorb is another unanswered question. This capacity to take up nutrients is important for the survival of the coral reefs since the seagrass meadows function as a buffer between them and the land. Corals would be impacted by excess nutrients and particularly by the resultant excess algal growth and could die off. This is an additional threat to the coral reefs of Hainan which are already impacted by overfishing as well as cyanide and dynamite fishing, similar to the Spermonde Archipelago.
- 2.45 > For decades, mercury-containing wastewater had been pumped into the bay off the Japanese fishing town of Minamata. Making its way through the food chain, the poison was ultimately ingested by humans.
Coastal waters as sewage basins
Coastal waters are not only impacted by excess nutrients but also by untreated sewage and industrial effluent. While wastewater treatment technologies in industrial nations tend to be highly developed and remove a high proportion of pollutants from wastewater before it enters rivers or the sea, there are many regions in developing countries in which wastewater treatment is insufficient. According to the World Bank, in Africa only about 10 per cent of wastewater reaches treatment facilities. Studies have shown that in the Ghanaian capital Accra untreated wastewater is responsible for the bacterial and viral load of rivers and other watercourses serving as drinking water sources for the population. Frequent cases of diarrhoea are the result. Approximately one quarter of all deaths of children aged under five years in the greater Accra area are attributed to this problem. Moreover, there have been repeated cases of cholera.
In many regions there is not only the threat from pathogens but also the problem of pollutants that directly enter the sea via rivers or sewers. These pollutants include heavy metals, for example from mining or metal production, as well as numerous compounds originating in the chemical industry. Several environmental disasters have shown just how dangerous these substances can be. One such case is that of Minamata, a port town in western Japan. In the 1950s, a local factory discharged mercury-containing wastewater into the sea. The poison was first taken up by algae. Then the algae were consumed by fish the local people valued particularly highly as culinary fish. The mercury concentration in the fish was so high that more than 10,000 people suffered from mercury poisoning. Thousands of them died. Today this type of severe mercury poisoning is known as Minamata disease.
A lot more than a “dirty dozen”
According to the Organisation for Economic Co-operation and Development (OECD), around 100,000 different chemical substances are being produced worldwide; in Europe alone about 10,000 of these are produced in quantities of more than 10 tonnes per year. Up to 3 per cent of the global production is of concern; these environmentally relevant pollutants include, for example, compounds of lead, mercury and other heavy metals arising in the course of mining, in industrial manufacturing processes and when burning heating oil.
Persistent organic pollutants (POPs) are particularly critical. They are defined by the following problematic characteristics: They are persistent and toxic, they accumulate in living organisms and they can also volatize into the atmosphere and travel long distances. Since POPs are strongly resistant to breaking down in the environment they can continue to enter the food chain for many years.
A group of twelve particularly dangerous compounds of this nature, known as the “dirty dozen”, were the first such substances to be banned worldwide under the Stockholm Convention. Polychlorinated biphenyls (PCBs) are among the twelve. Today a total of 24 substances are banned under the Convention.
Fighting fire with fire?
In 2007 the EU REACH Regulation (Registration, Evaluation, Authorisation and Restriction of Chemicals) entered into force in the European Union; it was adopted in order to improve the protection of human health and the environment from risks potentially posed by chemicals. The Regulation requires industrial companies manufacturing or using chemical substances to register these substances and provide evidence of their harmlessness. However, companies may put substances that have already been in the marketplace for some time to new uses without having to furnish any additional evidence.
Therefore, substances that are banned today on account of their toxicity may be replaced by established substances with similar characteristics. But these replacements may equally be of concern. Polybrominated diphenyl ethers (PBDEs) are an example of this problem. For a long time these bromium containing compounds were used as a flame retardant. Experts had found that PBDEs are persistent and carcinogenic, which is why they were banned some time ago. As an alternative, the industry then began to use Dechlorane Plus, an established substance originally used as an insecticide in the 1970s, the use of which in the outdoors had since been banned in the EU. Dechlorane Plus is persistent too and in water it attaches to suspended solids together with which it is primarily deposited in coastal sediments. Scientists have shown that eels in European coastal waters are contaminated with Dechlorane Plus.
- This example highlights the weakness in common practice whereby banned substances may be replaced with established substances that are similarly problematic. As a consequence, discussions are underway as to whether Dechlorane Plus should also be banned internationally under the Stockholm Convention. Denmark has launched an initiative to this effect.
A ban on chemicals posing environmental hazards is normally preceded by years of discussions. Countries in which the relevant substances are produced or processed often oppose a ban. However, the Stockholm Convention contains a provision under which particularly hazardous POPs can be banned within a shorter timeframe if they are extremely bioaccumulative and extremely persistent. These substances are termed very P/very B (very persistent/very bioaccumulative).
The chemical compound PFOS (perfluorooctane sulfonate) is an example of substances of this kind. It was primarily used in the textile industry, for example in the manufacturing of breathable membranes for outdoor jackets. But it was also used in the paper industry for the production of stain, grease and water repellent papers used for example in fast-food packaging. In addition it was used for surface treatments for furniture, carpets and clothing. Because of the persistent nature of PFOS it has strongly accumulated in nature. It has been detected in water, soils, air and living organisms worldwide. Comparatively high concentrations can be found in the top links of the food chain, such as fish, seals, marine birds and polar bears and of course also in humans.
When it became obvious at the end of the last century that PFOS are among the vP/vB compounds, the substance was banned. The chemically closely related compound PFOA (perfluorooctanoic acid) was similarly taken off the market. A period of only five years passed between various groups of researchers providing evidence of the substance’s potential hazardous nature and its ban. For other POPs that are not considered to be vP/vB this process can take up to 20 years.
Shifting problems
PFOS and PFOA primarily accumulate in the blood and liver. Following their ban, they were replaced by chemically closely related compounds in the perfluorocarbon group (PFCs) which includes PFOS and PFOA. The industry now uses PFCs that less strongly accumulate in the blood and liver and thus are less bioaccumulative. However, this poses a new problem: These PFCs are relatively well soluble in water. Studies have shown that concentrations of these water-soluble PFCs have increased strongly, especially in China’s rivers and coastal waters. The introduction of new PFCs has therefore only shifted the environmental problem from bioaccumulation in organisms to elevated concentrations in the water.
Regardless of the type of pollutant, it has been shown that the concentrations of many problematic substances in rivers and coastal waters in the EU and the USA have declined in recent years. This is due in part to improved wastewater treatment technologies and the improved treatment of industrial effluents but it is also due to the fact that the production and processing of many chemicals has been shifted from western industrialized nations to countries such as China and India. Therefore it is hardly surprising that the situation has worsened in these countries even though, at least in part, modern wastewater treatment technology is being used.
But even modern technology is not capable of completely removing all contaminants from wastewater. Given that China produces particularly large quantities of chemicals, the quantity of pollutants entering the environment remains relevant, including the total amount of PFCs. Many estuarine coastal areas are contaminated by PFCs, for example the Yangtze River Delta in eastern China. This is where the PFCs are produced and used by several textile companies. Other rivers along China’s east coast are also heavily polluted. The PFC concentration in the Xiaoqing River Delta, for example, is 2000 times as high as that found in the estuary of the Elbe River in Germany, a situation that is attributed first and foremost to the relocation of production to China. There has not yet been any in-depth research on the potential environmental impact of these high concentrations in the water or on the overall severity of this accumulation.
Extra Info Inland sludge spill contaminates the coast – the Rio Doce case

Surface mining poisons entire region
Large-scale mining operations are another significant contributor to pollution in rivers and coastal waters. Mostly these involve the mining of economically interesting chemical elements such as iron, copper or gold. Since these elements do not occur naturally in their elemental form but are bound to other elements they must be separated and concentrated. The resultant mining waste is deposited either as dry waste in spoil heaps or together with partially toxic wastewater and sludges in basins or tailings ponds. Time and again such basins and pits fail, releasing into the environment the substances they contain.
There are also cases where wastewater is directly discharged into rivers, one example being the Ok Tedi mine in Papua New Guinea which has discharged directly into the Ok Tedi and Fly rivers since the 1980s. These rivers, together with their tributaries, form one of the largest tropical river systems worldwide. At times the inland mine discharged such vast quantities of sludge into the rivers that it deposited on the riverbanks, polluting not only the river water but also the surrounding environment with copper residues in particular. It is assumed that the decline of the river’s fish populations is due to this contamination.
Similar environmental pollution is evident in the southwest Indian coastal region in the Panmana village area in the state of Kerala. Heavy-metal-rich placer deposits, mineral-rich sediments deposited over millions of years, have been mined here since 1922. The placer deposits were initially mined for metal. Since the 1980s, the interest has shifted to ilmenite, a titanium-iron oxide mineral. Ilmenite is the main source of the widely used whitener titanium dioxide, a pigment used in wall paints, automotive paint and toothpaste. Since 1984, ilmenite has been processed directly at a local factory. The resultant heavy metals are no longer used. Together with other chemical elements, the heavy metal-containing wastewater is discharged into storage basins which, however, have been leaking for more than a decade. During this time this leakage has slowly contaminated water wells and soils over an area of 16 square kilometres around the factory. The heavy metal concentrations in the area exceed international threshold values multiple times over. The contamination of soils and water not only result in plants dying in many places, but more and more people are suffering from excema and are getting cancer. Many of the local people have left their home region as a result.
- 2.47 > Heavy metal contamination is widespread in the soils in the village of Panmana in the Indian state of Kerala. Plants can hardly grow here anymore.

Mysterious marine litter
In recent years, scientists and the media have paid particularly strong attention to marine pollution caused by plastic waste, not least owing to the fact that this threat is often directly visible and the relationship between cause and effect is easily understood. Current discussions revolve around potential risks caused by the plastic debris and the question of how just much litter is floating around the oceans. Marine litter is categorized as follows:- macroplastics are greater than 25 millimetres in size,
- mesoplastics are 5 to 25 millimetres in size,
- large microplastics are 1 to 5 millimetres in size,
- small microplastics measure from only a few micro-metres up to 1 millimetre.
For some time now investigations have been underway on the impacts of microplastics on marine life. In a laboratory experiment, mussels were exposed to high concentrations of microparticles. The particles were absorbed from the digestive tract into tissues where they triggered inflammatory responses. These experiments have been criticized for working with extremely high particle concentrations, i.e. significantly higher than the concentrations found in the oceans. For comparative purposes, similar experiments were conducted in which the mussels were kept in water with significantly lower particle concentrations, i.e. concentrations similar to those found in the North Sea. The mussels suffered no evident damage in these experiments.
Waste beyond measure
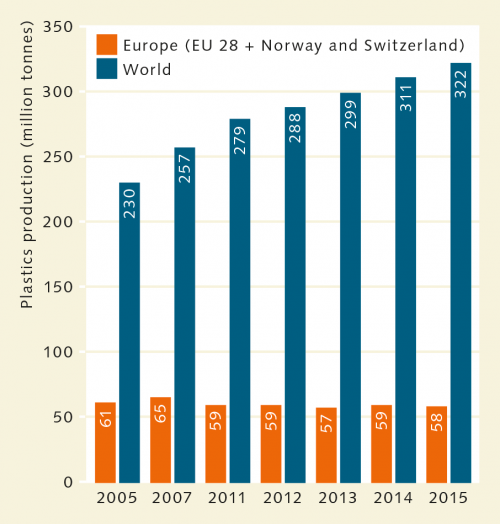
In general, it is impossible to precisely measure and quantify the amount of litter present in the oceans. Nonetheless, in 2015 US American scientists attempted to come up with an estimate as part of a study. To this end, they looked at the production side and calculated that the 300 million tonnes of plastic materials produced worldwide every year result in the generation of 275 million tonnes of plastic litter, i.e. approximately 90 per cent of the production. For their study, the researchers had analysed the existing waste disposal infrastructure and recycling quotas in a range of countries. From this information they deduced that approximately 4.8 to 12.7 million tonnes of plastic litter end up in the oceans each year. While these figures have often been cited since their publication, criticism has been levelled at the study to the effect that production data in conjunction with information on waste recycling do not allow for conclusions as to the quantities of waste that ultimately end up in the oceans, given that litter finds its way into the marine environment through very different pathways: by way of rivers, through direct disposal into the oceans, or by being blown out to sea from landfill sites. It is impossible to quantify all these pathways. Owing to the fact that a major proportion of the plastic waste has sunk to greater depth where it can no longer be discovered, it is similarly impossible to quantify the amount of waste that has entered the oceans in the past.
Exaggerated estimates?
Many different sources contribute microplastics to the marine environment: the slow degradation or disintegration of larger plastic marine litter items under the influence of saltwater and UV sunlight, ship coatings, abrasion from plastic items and car tyres, and also plastic microbeads in scrubs. The difficulty in determining the overall quantities of microplastics is primarily due to the fact that different groups of researchers have thus far used different methods and devices to record and study microplastics. Some scientists extrapolated particle concentrations in water to cubic metres, others to square kilometres. Some stated the absolute number of particles found while others stated their weight in milligrams per kilogram. As a result, the comparability of figures is very limited at present. To remedy this situation an EU project is underway which aims to develop the first harmonized measurement standards. These will concern not only the way waterborne particles are counted but also their correct identification. For a long time researchers have tried to use microscopes to record the number of particles.
- 2.48 > The amount of plastics produced worldwide has been increasing for years. It is reasonable to assume that the amount of plastic waste reaching the oceans has similarly increased. However, there are no reliable data.
- However, this optical method overestimated the quantity of particles by up to 70 per cent as quartz sand was often misidentified as plastic. New devices that use infrared light and are capable of precisely identifying plastics are to avoid such errors in the future.
Tourism: recreation at the expense of coastal habitats
While the risk to coastal habitats posed by plastic litter is as yet largely unknown, the adverse impacts of tourism have been evident for years. The construction of hotels and roads, especially in highly popular holiday regions, has considerably altered many coastal landscapes. Wetlands have been drained and built over and beaches are visited by high numbers of people. The organisms dependent on the coastal strip, i.e. the immediate transition area between water and land, are strongly impacted by these developments. Many bird species, for example, depend on coastal wetlands such as lagoons or estuaries as breeding or resting areas. Seals similarly use the coastal strip for hunting or resting, and marine turtles need pristine sandy beaches on which they can bury their eggs. In some regions such sites have become very rare.
- 2.49 > Intensiver Tourismus kann Korallenriffe stark beschädigen – beispielweise wenn Urlauber Meeresorganismen ritzen.

- At the beginning of the nineteenth century, many Mediterranean regions still hosted large populations of green sea turtles, loggerhead sea turtles and leatherback sea turtles. As a result of the transformation of natural sandy coastal areas into tourist resorts these species have almost completely disappeared. In the Mediterranean, green sea turtles can now only be found off Cyprus, loggerhead sea turtles have become limited to small areas off Greece and Turkey, and in exceptional cases leatherback sea turtles may still be found off Syria or Israel.
The transformation of natural coastal margins into tourist sites, some of which have taken on an urban character, also gives rise to other impacts on the coastal environment. In many places, concrete walls and harbour infrastructure have been built for the purposes of coastal protection, as seafront esplanades or as marinas. Such developments have completely altered the habitats of many different aquatic organisms. Caves, refuges and feeding grounds were lost. Even where the seashore is primarily rocky, concrete buildings alter biocoenoses. The chemical composition of the surfaces of concrete structures differs from that of natural stone. Many marine organisms that attach to solid surfaces therefore avoid concrete structures, which tend to be significantly less species-rich overall as a result.
Great pressure on coral reefs
The gradual destruction of coastal habitats is caused not only by building development but also by intensive tourism use. Coral reefs are among the heavily frequented habitats. The impacts of intensive diving tourism were studied in greater detail at the Great Barrier Reef on Australia’s East Coast. The reef was found to be subject to different types of destruction:- In areas where boats set off, corals are destroyed by holidaymakers wading from shore to boats and back. Corals are completely destroyed in heavily frequented sections. Anchored pontoons, floating restaurants and bars etc. permanently shade out sections of reefs. Corals die off in such sections.
- Anchors that are carelessly dropped by pleasure boats or diving boats may directly destroy corals.
- Zu Wasser gelassene Anker von Ausflugs- und Tauchbooten können Korallen zerstören.
- Where fish are fed for observation purposes, inappropriate or spoilt feed may result in the spread of diseases on the reef. Moreover, feeding may attract large predatory fish that do not normally frequent the reef sites concerned, which in turn leads to a significant decline in certain fish species.
- Divers, and inexperienced divers in particular, come into contact with reef material and break off especially the finely branched corals.



![fig. 2.35: © [M] mare, Fotos: © NASA image created by Jesse Allen Landsat 3 MSS data provided by the University of Maryland’s Global Land Cover Facility. Landsat 7 ETM+ data provided courtesy of the Landsat Project Science Office, NASA/ GSFC fig. 2.35:In the past 40 years the Pearl River Delta in China has developed from an agricultural to a highly industrialized and heavily populated region. The left side of the photomontage is a satellite image from the year 1979, and the right side of the image dates from 2003. Vegetation is shown in red and built-up areas in grey. Watercourses can be seen in blue. © [M] mare, Fotos: © NASA image created by Jesse Allen Landsat 3 MSS data provided by the University of Maryland’s Global Land Cover Facility. Landsat 7 ETM+ data provided courtesy of the Landsat Project Science Office, NASA/ GSFC](https://worldoceanreview.com/wp-content/uploads/2017/10/wor5_k2b_abb_2-35-150x186.jpg)
